Galileo, İki Yeni Bilim, Gün 3, Teorem 6
–Zeynel Ahmet
Daha önce VII. teoremi incelemiştik. Burada VI. teoreme bakıyoruz. Galileo'nun sözlerini blok alıntı olarak yazdım. Bu teoremin bir de "Mekanik ilkeleri kullanarak aynı sonuç elde edilebilir…" diye başlayan ikinci bölümü var, orayı daha sonra incelemeyi planlıyorum. (Teoremin tümünü inceleminin sonuna ekledim)
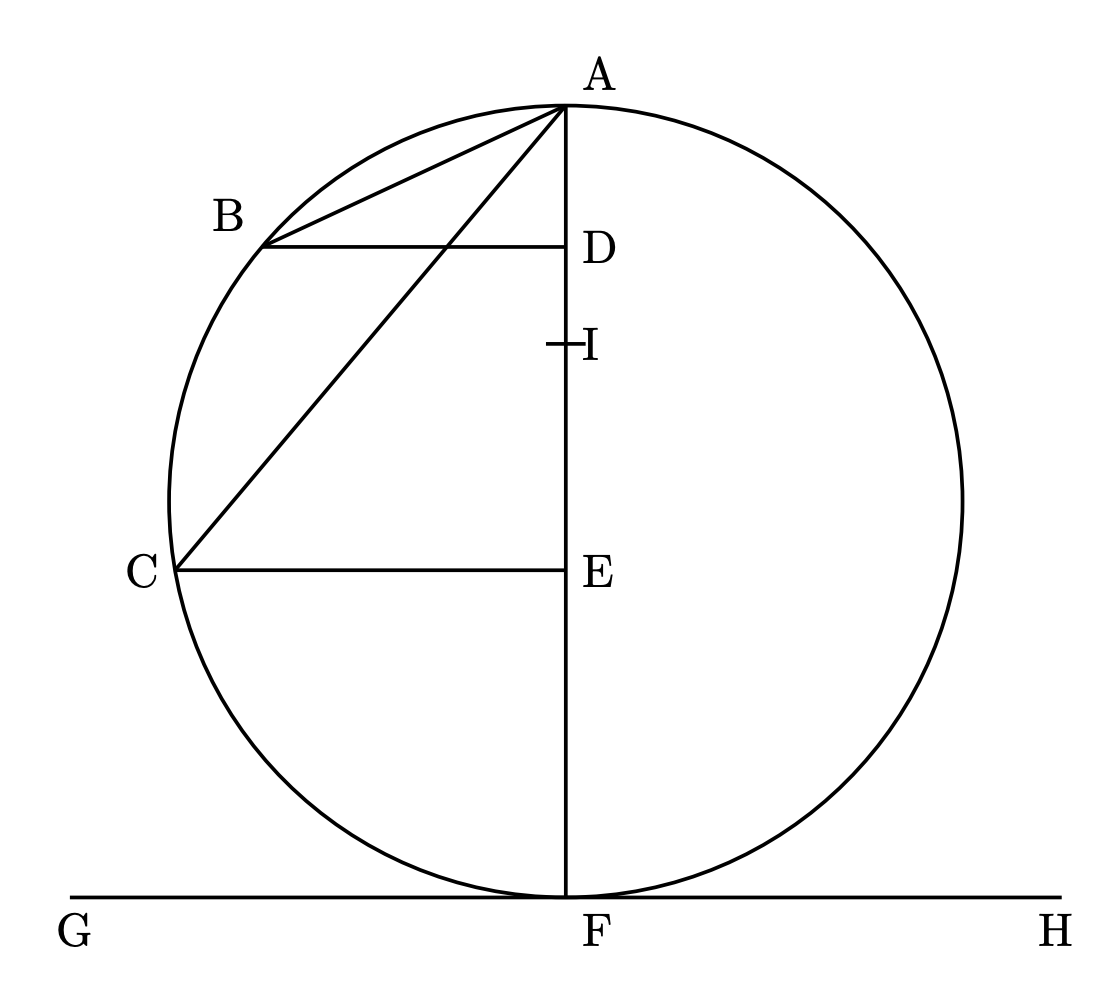
Figure 1: Teorem 6
TEOREM VI. ÖNERME VI
Dikey bir çemberin en yüksek ya da en alçak noktasından çevreyi kesen herhangi eğik düzlemler çizilirse, bu kirişler boyunca iniş zamanları birbirine eşittir.
\(BD\) ve \(CE\)'yi çapa dik çizin; düzlemlerin yükseklikleri \(AE\) ve \(AD\) arasında \(AI\)'yı orta orantılı yapın ve \(FA \cdot AE\) ve \(FA \cdot AD\) dikdörtgenleri sırasıyla \(AC\) ve \(AB\)'nin karelerine eşit olduğundan, \(FA \cdot AE\) dikdörtgeninin \(FA \cdot AD\) dikdörtgenine oranı \(AE\)'nin \(AD\)'ye oranı kadar olduğundan, \(AC\)'nin karesinin \(AB\)'nin karesine oranı \(AE\) uzunluğunun \(AD\) uzunluğuna oranı kadar olduğu çıkar.
(1)…Galileo bu orantıları yazıyor (benzer üçgenler \(AFC\) ve \(ACE\) ve \(AFB\) ve \(ADB\)'yi kullanarak):
\[FA \cdot AE = (AC)^2\]\[FA \cdot AD = (AB)^2 \](2)…Sonra,
\[\frac{FA \cdot AE}{FA \cdot AD} = \frac{AE}{AD}\](3)…Sadeleştirerek,
\[\frac{(AC)^2}{(AB)^2} = \frac{AE}{AD}\]çıkarımını yapıyor.
Fakat \(AE\) uzunluğunun \(AD\)'ye oranı \(AI\)'nin karesinin \(AD\)'nin karesine oranı kadar olduğundan, \(AC\) ve \(AB\) doğrularının karelerinin birbirine oranı \(AI\) ve \(AD\) doğrularının karelerinin oranı kadar olduğu, dolayısıyla \(AC\) uzunluğunun \(AB\) uzunluğuna oranının \(AI\)'nin \(AD\)'ye oranı kadar olduğu çıkar.
(4)…Galileo bu orantıyı yazıyor:
\[\frac{AE}{AD} = \frac{(AI)^2}{(AD)^2}\]
(5)…Galileo bu orantıyı \(EA\) ve \(AD\) arasındaki \(AI\) orta orantılısından buluyor. Orta orantılı tanım gereği, \(AI\), \(AE\) ile \(AD\)’nin geometrik ortalamasıdır; bu yüzden,
\[(AI)^2 = AE \cdot AD\](6)…İki tarafı \((AD)^2\)'ye böldüğümüzde:
\[\frac{(AI)^2}{(AD)^2} = \frac{AE\cdot \cancel{AD}}{(AD)^\cancel{2}} = \frac{AE}{AD}\](7)…(3)'le (4)'ü birleştirelim,
\[\frac{(AC)^2}{(AB)^2} = \frac{(AI)^2}{(AD)^2}\](8)…Karelerin oranı, uzunlukların oranının karesiyle aynı:
\[\left (\frac{AC}{AB}\right )^2 = \left (\frac{AI}{AD}\right )^2\](9)…Dolayısıyla,
\[\frac{AC}{AB} = \frac{AI}{AD}\]
Fakat daha önce \(AC\) boyunca düşüş süresinin \(AB\) boyunca düşüş süresine oranının, \(AC\)'nin \(AB\)'ye ve \(AD\)'nin \(AI\)'ye oranlarının çarpımına eşit olduğu gösterilmişti; fakat bu son oran \(AB\)'nin \(AC\)'ye oranı ile aynıdır.
Dolayısıyla \(AC\) boyunca düşüş süresinin \(AB\) boyunca düşüş süresine oranı, \(AC\)'nin \(AB\)'ye ve \(AB\)'nin \(AC\)'ye oranlarının çarpımıdır.
Bu sürelerin oranı bu nedenle birdir. Böylece önermemiz çıkar.
(10)…Galileo 5. teoremde bu sonucu bulmuştu:
\[\frac{t_{AC}}{t_{AB}} = \frac{AC\cdot AD}{AB\cdot AI}\](11)…Yukarda (9)'da bulduğumuz \(AC/AB = AI/AD\)'nin tersini alalım:
\[\frac{AB}{AC} = \frac{AD}{AI}\](12)…(10)'da \(AD/AI \Longrightarrow AB/AC\) değişimini yapalım:
\[\frac{t_{AC}}{t_{AB}} = \frac{\cancel{AC}\cdot \cancel{AB}}{\cancel{AB}\cdot \cancel{AC}} = 1\](13)…Böylece, Galileo’nun iddia ettiği gibi, farklı kirişler boyunca iniş sürelerinin eşit olduğu ispatlanmış oldu:
\[t_{AC} = t_{AB}\]
**
Teoremin tümü
TEOREM VI. ÖNERME VI
Dikey bir çemberin en yüksek ya da en alçak noktasından çevreyi kesen herhangi eğik düzlemler çizilirse, bu kirişler boyunca iniş zamanları birbirine eşittir.
\(GH\) yatay doğrusu üzerinde dikey bir daire çizin. En alt noktasından - yatay ile teğet noktasından - \(FA\) çapını çizin ve en üst nokta \(A\)'dan, çevre üzerindeki herhangi noktalar olan \(B\) ve \(C\)'ye eğik düzlemler çizin; o zaman bunlar boyunca düşüş süreleri eşittir.
\(BD\) ve \(CE\)'yi çapa dik çizin; düzlemlerin yükseklikleri \(AE\) ve \(AD\) arasında \(AI\)'yi orta orantılı yapın; ve \(FA \cdot AE\) ve \(FA \cdot AD\) dikdörtgenleri sırasıyla \(AC\) ve \(AB\)'nin karelerine eşit olduğundan, \(FA \cdot AE\) dikdörtgeninin \(FA \cdot AD\) dikdörtgenine oranı \(AE\)'nin \(AD\)'ye oranı kadar olduğundan, \(AC\)'nin karesinin \(AB\)'nin karesine oranı \(AE\) uzunluğunun \(AD\) uzunluğuna oranı kadar olduğu çıkar.
Fakat \(AE\) uzunluğunun \(AD\)'ye oranı \(AI\)'nin karesinin \(AD\)'nin karesine oranı kadar olduğundan, \(AC\) ve \(AB\) doğrularının karelerinin birbirine oranı \(AI\) ve \(AD\) doğrularının karelerinin oranı kadar olduğu, dolayısıyla \(AC\) uzunluğunun \(AB\) uzunluğuna oranının \(AI\)'nin \(AD\)'ye oranı kadar olduğu çıkar.
Fakat daha önce \(AC\) boyunca düşüş süresinin \(AB\) boyunca düşüş süresine oranının, \(AC\)'nin \(AB\)'ye ve \(AD\)'nin \(AI\)'ye oranlarının çarpımına eşit olduğu gösterilmişti; fakat bu son oran \(AB\)'nin \(AC\)'ye oranı ile aynıdır.
Dolayısıyla \(AC\) boyunca düşüş süresinin \(AB\) boyunca düşüş süresine oranı, \(AC\)'nin \(AB\)'ye ve \(AB\)'nin \(AC\)'ye oranlarının çarpımıdır.
Bu sürelerin oranı bu nedenle birdir. Böylece önermemiz çıkar.
Mekanik ilkeleri kullanarak aynı sonuç elde edilebilir, yani düşen bir cismin \(CA\) ve \(DA\) mesafelerini geçmek için eşit süreler gerektireceği, aşağıdaki şekilde gösterildiği gibi.
\(BA\)'yı \(DA\)'ya eşit ayır ve \(BE\) ile \(DF\) diklerini indir; mekanik ilkelerden, eğik \(ABC\) düzlemi boyunca etkiyen momentum bileşeninin toplam momentuma oranının \(BE\)'nin \(BA\)'ya oranı kadar olduğu çıkar; benzer şekilde \(AD\) düzlemi boyunca momentum, toplam momentumuna oranı \(DF\)'nin \(DA\)'ya, yani \(BA\)'ya oranı kadardır.
Dolayısıyla aynı ağırlığın \(DA\) düzlemi boyunca momentumu, \(ABC\) düzlemi boyunca momentuma oranı \(DF\) uzunluğunun \(BE\) uzunluğuna oranı kadardır; bu nedenle, aynı ağırlık birinci kitabın ikinci önermesine göre eşit sürelerde, \(CA\) ve \(DA\) düzlemleri boyunca \(BE\) ve \(DF\) uzunluklarının birbirine oranı kadar mesafeler geçecektir. Fakat \(CA\)'nın \(DA\)'ya oranının \(BE\)'nin \(DF\)'ye oranı kadar olduğu gösterilebilir. Böylece düşen cisim iki \(CA\) ve \(DA\) yolunu eşit sürelerde geçecektir.
Dahası, \(CA\)'nın \(DA\)'ya oranının \(BE\)'nin \(DF\)'ye oranı kadar olduğu gerçeği şu şekilde gösterilebilir: \(C\) ve \(D\)'yi birleştir; \(D\)'den, \(AF\)'ye paralel \(DGL\) doğrusunu çiz ve \(AC\) doğrusunu \(I\)'de kessin; \(B\)'den \(BH\) doğrusunu çiz, yine \(AF\)'ye paralel.
O zaman \(\angle ADI\) açısı \(\angle DCA\) açısına eşit olacaktır, çünkü \(LA\) ve \(DA\) eşit yaylarını görürler, ve \(\angle DAC\) açısı ortak olduğundan, \(\triangle CAD\) ve \(\triangle DAI\) üçgenlerinin ortak açının etrafındaki kenarları birbirine orantılı olacaktır; buna göre \(CA : DA = DA : IA\), yani \(BA : IA\), yani \(HA : GA\), yani \(BE : DF\) kadardır.
Quod erat demonstrandum.
Aynı önerme daha kolay şu şekilde gösterilebilir: \(AB\) yatay doğrusu üzerinde çapı \(DC\) dikey olan bir daire çiz.
Bu çapın üst ucundan çevreyle buluşmaya uzanan herhangi bir eğik düzlem \(DF\) çiz; o zaman, bir cismin \(DF\) düzlemi boyunca düşmesinin \(DC\) çapı boyunca düşmesi ile aynı süreyi alacağını söylüyorum.
\(FG\)'yi \(AB\)'ye paralel ve \(DC\)'ye dik çiz; \(FC\)'yi birleştir; ve \(DC\) boyunca düşüş süresi \(DG\) boyunca düşüş süresine, \(CD\) ve \(GD\) arasındaki orta orantılının \(GD\)'nin kendisine oranı kadar olduğundan; ve aynı zamanda \(DF\), \(DC\) ve \(DG\) arasında orta orantılı olduğundan, yarı daire içine yazılan \(\angle DFC\) açısı dik açı olduğundan ve \(FG\), \(DC\)'ye dik olduğundan, \(DC\) boyunca düşüş süresinin \(DG\) boyunca düşüş süresine oranının \(FD\) uzunluğunun \(GD\)'ye oranı kadar olduğu çıkar.
Fakat \(DF\) boyunca düşüş süresinin \(DG\) boyunca düşüş süresine oranının \(DF\) uzunluğunun \(DG\)'ye oranı kadar olduğu zaten gösterilmişti; dolayısıyla \(DF\) ve \(DC\) boyunca düşüş süreleri, \(DG\) boyunca düşüş süresi ile aynı oranı taşır; sonuç olarak eşittirler.
Benzer şekilde, çapın alt ucundan \(CE\) kirisini çizerse, aynı zamanda ufka paralel \(EH\) doğrusunu çizerse ve \(E\) ile \(D\) noktalarını birleştirirse, \(EC\) boyunca düşüş süresinin \(DC\) çapı boyunca düşüş süresi ile aynı olacağı gösterilebilir.
SONUÇ I
Buradan, \(C\) veya \(D\)'den çizilen tüm kirişler boyunca düşüş sürelerinin birbirine eşit olduğu çıkar.
SONUÇ II
Aynı zamanda, herhangi bir noktadan dikey bir çizgi ve düşüş süresinin aynı olduğu eğik bir çizgi çizilirse, eğik çizginin dikey çizginin çap olduğu yarı dairenin bir kirişi olacağı da çıkar.
SONUÇ III
Dahası, bu düzlemlerin eşit uzunluklarının dikey yükseklikleri düzlemlerin uzunluklarının kendileri gibi birbirine orantılı olduğunda, eğik düzlemler boyunca düşüş süreleri eşit olacaktır; böylece, son önceki şekilde \(CA\) ve \(DA\) boyunca düşüş sürelerinin, \(AB\)'nin dikey yüksekliği (\(AB\), \(AD\)'ye eşit olmak üzere), yani \(BE\)'nin, \(DF\) dikey yüksekliğine oranı \(CA\)'nın \(DA\)'ya oranı kadar olması koşuluyla, eşit olduğu açıktır.