Gün 3, Teorem 7
Galileo’nun İki Yeni Bilim adlı kitabında üçüncü günün konusu ağırlıklı olarak eğik düzlemler ve serbest düşüş hareketidir. Burada Galileo, cismin bir eğik düzlem üzerindeki iniş süresinin hangi büyüklüklere bağlı olduğunu geometrik yöntemlerle incelemeye çalışır.
Bu yazıda 3. Gün’de yer alan 7. Teorem’i ele alacağız. Teorem, özel bir orantı kurulduğunda iki farklı eğik düzlem üzerindeki iniş sürelerinin eşit olduğunu gösteriyor. Galileo’nun geometriyle fiziği nasıl birleştirdiğini görmek için oldukça güzel bir örnek.
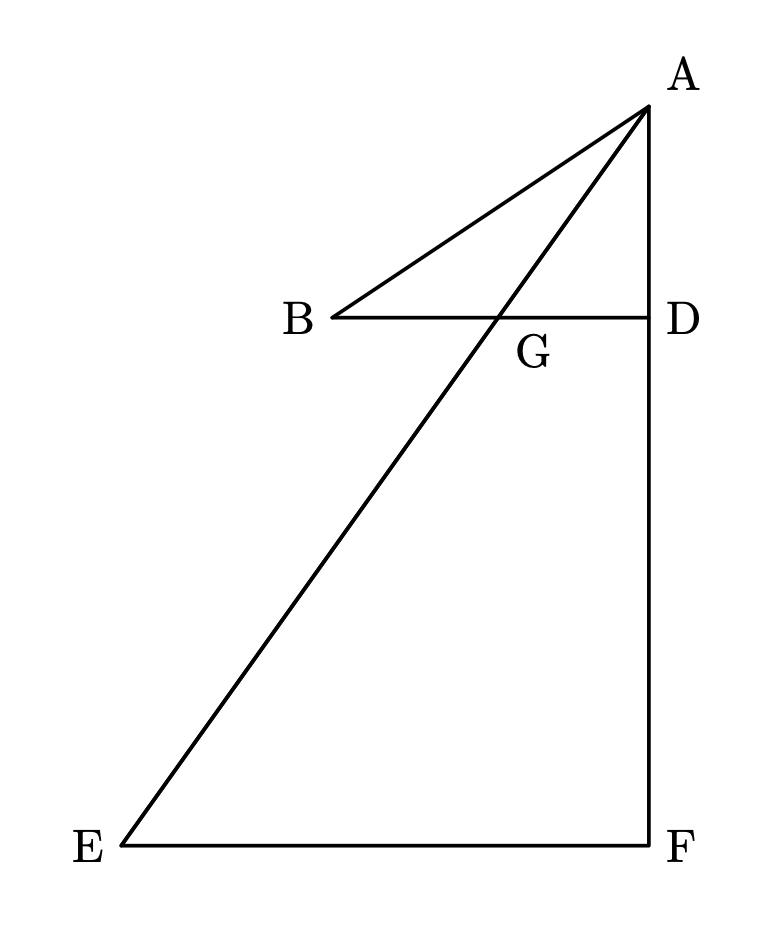
Figure 1: Teorem 7
Teoremin tam metni
Galileo'nun İki Yeni Bilim Kitabı, 3. Gün, 7. Teorem, 7. Önerme
(Crew ve de Salvio tercümesinde, sayfa, 194-195)
İfade:
Eğer iki eğik düzlemin yükseklikleri, uzunluklarının kareleri ile aynı oranda ise, hareketsiz durumdan başlayan cisimler bu düzlemleri eşit sürelerde kateder.
İspat:
Farklı uzunluklara ve farklı eğimlere sahip iki düzlem alalım, \(AE\) ve \(AB\), ki bunların yükseklikleri sırasıyla \(AF\) ve \(AD\) olsun: \(AF\) ile \(AD\) arasındaki oran, \(AE\)’nin karesi ile \(AB\)’nin karesi arasındaki oranla aynı olsun; o zaman, derim ki, \(A\) noktasından hareketsiz durumdan başlayan bir cisim, \(AE\) ve \(AB\) düzlemlerini eşit sürelerde kateder.
Düşey bir çizgiden, yatay paralel çizgiler \(EF\) ve \(DB\)’yi çizelim, ki \(DB\) çizgisi \(AE\) düzlemini \(G\) noktasında kessin.
\[FA:DA = (EA)^2:(BA)^2\]
olduğundan ve
\[FA:DA = EA:GA \]
olduğundan, buradan
\[EA:GA = (EA)^2:(BA)^2 \]
sonucu çıkar.
Dolayısıyla, \(BA\), \(EA\) ile \(GA\) arasında bir orta orantılıdır.
Şimdi, \(AB\) boyunca iniş süresi, \(AG\) boyunca iniş süresine, \(AB\)’nin \(AG\)’ye oranına eşit bir oranda bağlıdır ve ayrıca \(AG\) boyunca iniş süresi, \(AE\) boyunca iniş süresine, \(AG\)’nin \(AG\) ile \(AE\) arasındaki orta orantılıya, yani \(AB\)’ye oranına eşittir. Buradan, ex aequali (eşitlikten), \(AB\) boyunca iniş süresi, \(AE\) boyunca iniş süresine, \(AB\)’nin kendisine oranına eşittir.
Bu nedenle süreler eşittir.
Q.E.D.
İspatın mantığı
Teoremin şartı
Farklı uzunluklara ve farklı eğimlere sahip iki düzlem alalım, \(AE\) ve \(AB\), ki bunların yükseklikleri sırasıyla \(AF\) ve \(AD\) olsun: \(AF\) ile \(AD\) arasındaki oran, \(AE\)’nin karesi ile \(AB\)’nin karesi arasındaki oranla aynı olsun; o zaman, derim ki, \(A\) noktasından hareketsiz durumdan başlayan bir cisim, \(AE\) ve \(AB\) düzlemlerini eşit sürelerde kateder.
Yani,
\[AF : AD = (AE)^2 : (AB)^2\]Eğik düzlemler bu orantılarda inşa edilirlerse \(AB\) ve \(AE\) üzerinde düşüş süreleri aynı olacaktır.
Geometrik ilişki
İspata başlarken Galileo Öklid'den VI.2'yi kullanıyor:
\[AF : AD = AE :AG\]Yani, \(AFE\) üçgeninde, \(FE\)'ye paralel çizilen \(BD\) çizgisi karşılıklı kenarları orantılı olarak bölüyor.
Çıkarım
Bu iki ifadede \(AF : AD\)'ye eşit olan iki orantıyı birleştiriyoruz:
\[AE : AG = (AE)^2 : (AB)^2\]
Orta orantılı
\(AB\), \(AE\) ve \(AG\) arasında orta orantılıdır:
\[(AB)^2 = AE \times AG\]
Bu sonuç bir önceki orantıdan çıkıyor. Çapraz çarpım yapalım:
\[(AB)^2\times \cancel{AE} = AG\times (AE)^\cancel{2}\]
Yani,
\[(AB)^2= AE\times AG\]
\(AB\), \(AE\) ve \(AG\) arasında orta orantılıdır.
İniş süreleri
\(AB\) ve \(AG\) üzerinde iniş süresi
\[t_{AB} : t_{AG} = AB : AG\]
\(AG\) ve \(AE\) üzerinde iniş süresi
\[t_{AG} : t_{AE} = AG : AB\]
Ex aequali
\[\frac{t_{AB}}{\cancel{t_{AG}}} \times \frac{\cancel{t_{AG}}}{t_{AE}} = \frac{\cancel{AB}}{\cancel{AG}} \times \frac{\cancel{AG}}{\cancel{AB}} \Longrightarrow \frac{t_{AB}}{t_{AE}} = 1\]
Q.E.D
\(t_{AB} : t_{AE}= 1\) olduğuna göre,
\[t_{AB} = t_{AE}\]Sorular
Galileo neden \(t_{AG} : t_{AE} = AG : AB\) yazıyor?
Galileo'nun kendi bulduğu serbest düşüş yasasına göre
\[t_{AG} : t_{AE} = \sqrt{AG} : \sqrt{AE}\]olması gerekiyor çünkü, aynı düzlem üzerinde serbest düşüşte,
\[\text{düşüş süresi}\propto \sqrt{\text{uzunluk}}\]Peki Galileo düşüş sürelerini yanlış mı yazmış? Hayır Galileo, kareköklerle çalışmıyor, \(\sqrt{AG} : \sqrt{AE}\) ifadesini basit bir oran olarak, \(x/y\), şeklinde ifade etmek istiyor. Bunun içinde, orta oranlı kavramını kullanıyor:
\[(AB)^2 = AG \times AE\]\(AB\), \(AG\) ve \(AE\) arasında orta orantılıdır.
Orta orantılı ilişkisini kullanarak, Galileo'nun geometrik orantısı \(AG : AB\)'nin, serbest düşüş yasası \(\sqrt{AG} : \sqrt{AE}\) ile aynı olduğunu gösterebiliriz:
Geometrik oranın karesini alalım:
\[\left ( \frac{AG}{AB}\right)^2 = \frac{(AG)^2}{(AB)^2}\]\((AB)^2\) yerine \(AG\times AE\) yazalım,
\[\left ( \frac{AG}{AB}\right)^2 = \frac{(AG)^\cancel{2}}{\cancel{AG}\times AE} = \frac{AG}{AE}\]Böylece, şunu ispatlamış olduk,
\[\left ( \frac{AG}{AB}\right)^2 = \frac{AG}{AE}\]Karekök alalım,
\[ \frac{AG}{AB} = \frac{\sqrt{AG}}{\sqrt{AE}}\]Galileo'nun yazdığı geometric oranın (\(AG/AB\)) serbest düşüş yasası \((\sqrt{AG}/\sqrt{AE})\) ile birebir eşit olduğunu göstermiş olduk.
Galileo neden \(t_{AB} : t_{AG} = AB : AG\) yazıyor?
Burada, bir önceki soruda olduğu gibi Galileo, eğik düzlem üzerinde serbest düşüş yasasını kullanmıyor gibi gözüküyor. Eğik düzlem üzerinde serbest düşüş yasası,
\[t \propto \frac{\text{uzunluk}}{\sqrt{\text{yükseklik}}}\]Yani, bizim geometriye göre, Galileo,
\[\frac{t_{AB}}{t_{AG}} = \frac{AB/\sqrt{AD}}{AG/\sqrt{AD}}\]yazmalıydı.
Fakat burada açıkça görüyoruz ki, yükseklikler aynı olduğu için, \(\sqrt{AD}\) terimleri eleniyor. Yani, Galileo'nun ifadesi doğru!
Sonuç
Galileo’nun bu teoremi ilk bakışta modern serbest düşüş yasasıyla çelişiyor gibi görünebilir. Çünkü biz bugün, eğik düzlem üzerindeki sürelerin\[t \propto \frac{\text{uzunluk}}{\sqrt{\text{yükseklik}}}\]ilişkisine uyduğunu biliyoruz. Ancak Galileo “karekök” diliyle değil, geometri diliyle konuşuyor: orta orantılı kavramını kullanarak, modern fiziğin öngördüğü karekök oranlarını eşdeğer bir biçimde ifade ediyor.Böylece görüyoruz ki Galileo’nun geometrik ispatı aslında serbest düşüş yasasıyla tamamen uyumludur. Onun yaptığı şey, hareketi cebirsel formüllerle değil, klasik orantılar ve ex aequali kuralı ile açıklamaktır. Bu yaklaşım, 17. yüzyılda geometri ile fiziğin nasıl iç içe geçtiğini ve Galileo’nun bilim tarihindeki özel yerini çok güzel yansıtır.Özet
Galileo'nun bu güzel teoremi bu 7 adımda özetlenebilir:
(1) Önermenin şartı
\(AF : AD = (AE)^2 : (AB)^2\)
(2) Öklid VI.2
\(AF :AD = AE : AG\)
(3) Çıkarım
\(AE : AG = (AE)^2 : (AB)^2\)
(4) Orta orantılı
\((AB)^2 = AE\times AG\)
(5) İniş süresi (AB, AG üzerinden)
\(t_{AB} : t_{AG} = AB : AG\)
(6) İniş süresi (AG, AE üzerinden)
\(t_{AG} : t_{AE} = AG : AB\)
(7) Ex aequali
\((t_{AB} : \cancel{t_{AG}})\times \cancel{t_{AG}} : t_{AE} = \cancel{AB} : \cancel{AG} \times \cancel{AG} :\cancel{AB}\)
\(\Longrightarrow t_{AB} : t_{AE} = 1\)
\(\Longrightarrow t_{AB} = t_{AE}\)
Q.E.D