‎

Orbit

Orbit

Period and velocity

In circular motion, the period and velocity are closely related because the period describes how long it takes for an object to complete one full revolution, while velocity tells us how fast the object is moving along its circular path.

Definitions:

Period ($ T $): The time it takes for one complete revolution or cycle, measured in seconds.
Tangential Velocity ($ v $): The speed of an object moving along the circular path, measured in meters per second (m/s).

Relation between Period and Velocity

For an object in circular motion, the tangential (linear) velocity $ v $ is related to the period $ T $ by the formula:
\[ v = \frac{2\pi r}{T} \]
where:

$ r $ is the radius of the circular path,
$ T $ is the period.

Explanation

The distance traveled in one complete revolution is the circumference of the circle, $ 2\pi r $.
Since the period $ T $ is the time to travel this circumference, dividing the distance $ 2\pi r $ by the time $ T $ gives the velocity $ v $.

Inverse Relationship

Notice that $ v $ and $ T $ are inversely proportional:
\[ T = \frac{2\pi r}{v} \]
So, as the velocity $ v $ increases, the period $ T $ decreases, meaning the object completes its circular path faster. Conversely, a slower velocity results in a longer period.

This relationship is fundamental in circular motion and applies in various contexts, from the orbits of planets to the motion of objects on a rotating platform.

Are orbits forced or not forced

Newton says that orbits are created by bending straight lines into closed curves. So Newtonian orbit is forced.
For Aristotle and Galileo orbits are not forced because circular motion is natural motion

The difference between an eccentric orbit and an elliptical orbit

can we know the difference?
There is this figure in Densmore p.349

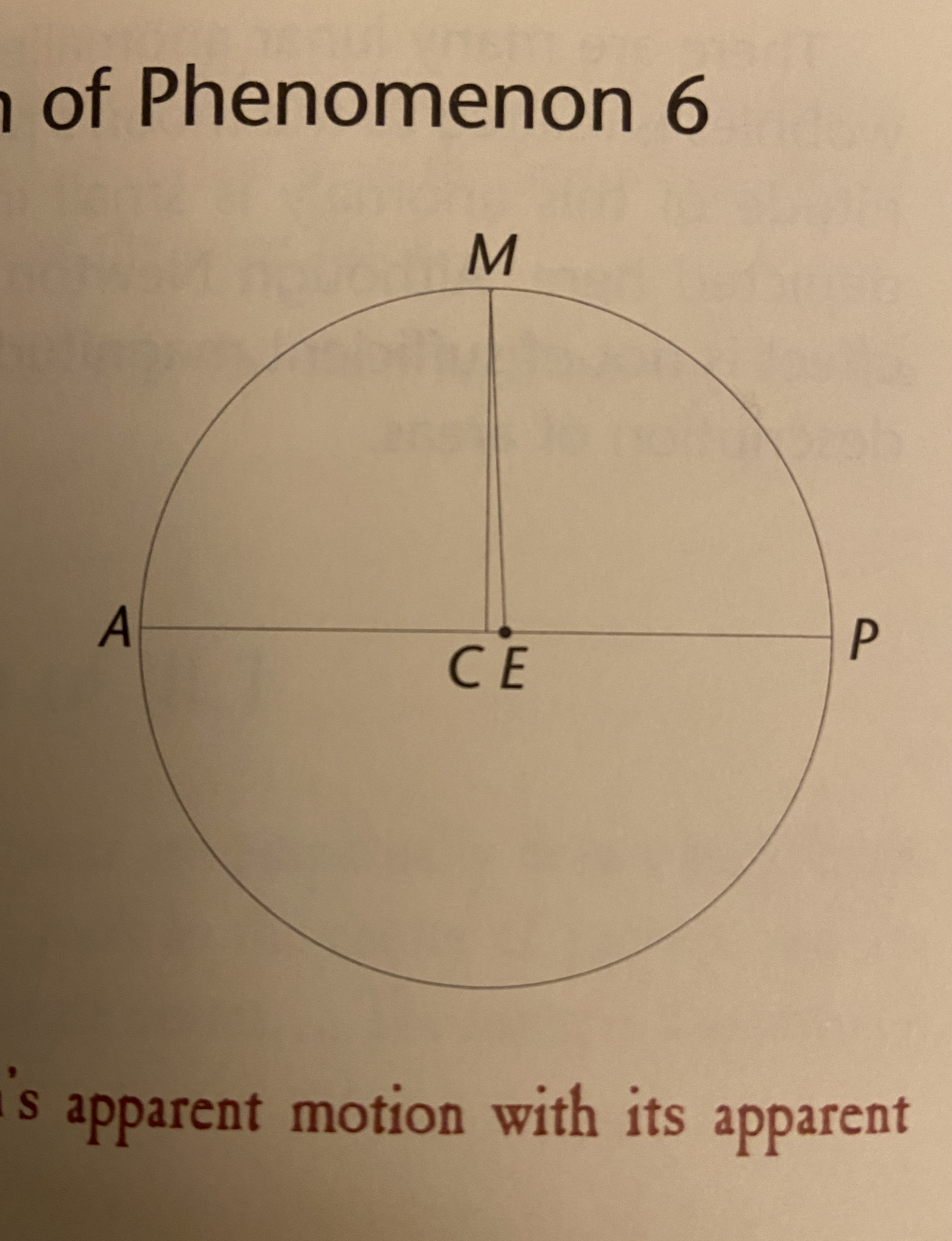
Figure 1: Moon’s orbit to scale

Densmore explains:

This diagram shows the earth-moon system, drawn to scale. The moon $M$ is shown at its mean distance (slightly greater than 60 earth radii). $A$ is its apogee, $P$ is its perigee, and $C$ is the center of its orbit. The orbit (whose eccentricity is $.0549) differs from circularity by less than the thickness of the lines in this diagram.

So the eccentricity of the moon’s orbit is due to its eccentricity not to the eccentricity of its “elliptical” orbit. In practice the moon’s orbit is circular.
I think the same will be true for the orbit of the earth.

Do planets need a force to hold them in orbit

Ancient astronomers taught that planets would fall to earth if they were not held in their orbits by something. And they came up with crystalline spheres to hold planets in orbits.
Newtonians reason similarly. They think that we need a force to hold planets in their orbits. Their “crystalline sphere” is Newton’s occult force. Just like crystalline spheres Newton’s occult force does not exist in nature.

Bi-elliptic transfer

Wikipedia page
They use ultimately kepler’s rule
John D. Cook webpage (submission at HN) other references too

Planetary orbits are practically circular

Planetary orbits are nearly circular
The most eccentric orbit is the orbit of Mercury and I’m not sure if it is circular and eccentric or elliptical

Table of Contents